
割合の計算@小学5生
1学期がもうすぐ終わろうとしています。
今回は「数学・算数の割合」についてです。
小学6年生の「分数の掛け算・割り算の文章題」、
中学1年生の「文字式の文章から式を立てる問題」、
中学2年生の「連立方程式の文章題」などができていない場合、
この「割合」の単元を復習すると、とても効果的です。
ぜひ、夏休みが始まるまでに復習してください。
割合の換算
割合の解き方で大切なポイントは2つあります。
1つ目は割合の換算です。
割合の換算とは、歩合・百分率・小数・分数をそれぞれきちんと変換することです。
| 少数 | 1 | 0.1 | 0.01 | 0.001 |
|---|---|---|---|---|
| 分数 | 1 | 10分の1 | 100分の1 | 1000分の1 |
| 百分率 | 100% | 10% | 1% | 0.1% |
| 歩合 | 10割 | 1割 | 1分 | 1毛 |
上の表はそれぞれの換算を表にしたものです。
この表を参考にして、次の(1)〜(9)の問題にチャレンジしてください。
割合の換算問題
| 小数 | 1 | (1) | (2) | (3) |
| 分数 | 1 | (4) | 4分の3 | (5) |
| 百分率 | 100% | 20% | (6) | (7) |
| 歩合 | 10割 | (8) | (9) | 1割2分5厘 |
式をたてる
割合を理解する2つ目のポイントは「式を立てる」です。
まずはく・も・わです。
小学校の教科書では、くらべる量・もとにする量・割合の3つを判別します。
割合=くらべる量÷もとにする量
もとにする量=くらべる量÷割合
そして、この3つの公式を暗記し、式をたてます。
この判別と、公式の暗記をしないと式がたてれないので、
生徒たちが「割合が難しい」と感じます。
それでは、簡単にできる方法を紹介します。
まず、くらべる量・もとにする量・割合の3つを判別を簡単にする方法です。
くらべる量:「〜は」
割合:単位がない。もしくは%、歩合になっているもの。
次に公式の暗記です。
公式の暗記は図にするとわかりやすいです。
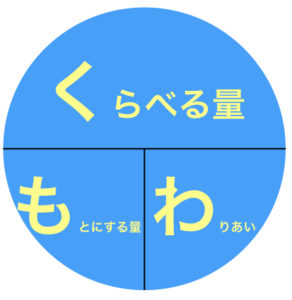
たては上÷下の割り算。よこはかけ算です。ただし割合は小数に換算します。
では、実際に練習してみましょう。
割合の文章問題
(1)4.6kgの6%は何kgですか。
(2)60円の25割は何円ですか?
(3)24㎞は60㎞の何%ですか?
(4)210人は何人の42%ですか?
(5)410mの5%の1割は何mですか?
もっと簡単な方法は?
上記の方法では、できない生徒もいます。
そんな時のとっておきの裏技も紹介します。
「〜は」を=(イコール)
それぞれ×と=にして式を立てます。
例えば先ほどの問題で式をたててみると、
(1)4.6kgの6%は何kgですか。
4.6×0.06=?
(2)60円の25割は何円ですか?
60×25=?
(3)24㎞は60㎞の何%ですか?
24=60×?
と式を立てます。
あとは計算のやり方をつたえます。
2×3=6
2がわからないときは6÷3
3がわからないときは6÷2
2の場所も3の場所も両方とも割り算でもとめられます。
24=60×?の場合
24÷60となり答えは0.4になります。
最後に
このような割合の基礎がわかると、次は、何%増しや何%減少などの問題にチャレンジします。
そのあと、速さの問題に取り組むとスムーズに理解できるようになります。
1学期にできなかったことは1学期のうちに理解し、できるようになるまで練習しましょう。
◎割合の換算の答え
(1)0.2(2)0.75(3)0.125(4)5分の1(5)8分の1(6)75%(7)12.5%(8)2割(9)7割5分
(7)ポイント:小数点の位置がきちんと理解できているか。
◎割合の文章題の答え
(1)4.6×0.06=0.276 答え0.276kg(ポイント:小数の掛け算で小数点の位置がきちんと理解できているか。)
(2)60×2.5=150 答え150円(ポイント:25割を小数に換算できているか。)
(3)24÷60=0.4 0.4×100=40 答え40%(ポイント:くらべる量÷もとにする量と小数から百分率に)
(4)210÷0.42=500 答え500人(ポイント:くらべる量を判別できるか)
(5)410×0.05=20.5 20.5×0.1=2.05 答え2.05m(「〜の」「〜の」ともとにする量が2回でてくる)




COMMENT ON FACEBOOK